Suites et Probabilités, exercice 5 - Annales de concours

Partager l'article

Cinquième exercice et avant dernière exercice dans la dernière ligne droite jusqu’à mardi prochain ! J’en publierai un dernier ce samedi midi, et vous pourrez me poser toutes les questions de dernière minute qui vous taraudent. Ensuite il faudra se reposer le dernier dimanche avant les écrits : inutile d’aborder les épreuves en étant fatigués ! Cette fois-ci, j’ai choisi un exercice que je trouve bien conçu pour réviser deux des thèmes au programme, à savoir les suites et les probabilités.

Comme toujours, on va retomber sur les immanquables du concours. La partie probabilités fera intervenir les deux formules très importantes à savoir utiliser :

La formule dite ‘”Formule de Bayes” : $p(A \cap B) = p_A(B) \times p(A) = p_B = p_B(A) \times p(B)$
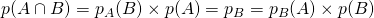
La formule dite “des probabilités totales” : $p(A) = p(A \cap B) + p(A \cap \overline{B})$ .

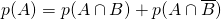Pour les suites, on est ici sur une utilisation des suites géométriques, dont il faut savoir utiliser les formules principales (expression de $u_n$ en fonction de $n$ , …).

Bref, un exercice sans difficulté majeur. Quoique, si, quand même : il y a un petit piège vicieux. Je suis sympa quand même, je vous dis qu’il y en a un…. mais je ne vous dit pas où ! (Un jour, je ferai un billet sur comment j’ai appris à mes élèves la définition du mot “Sadique”, condition nécessaire mais non suffisante pour devenir enseignant de mathématiques).

Allez, on se retrousse les manches, on attaque le sujet, et on ne touche pas à la correction avant d’avoir essayé, comme d’habitude !

Énoncé de l’exercice

Une entreprise a 1586 employés. Pour leur rendre service, elle a mis en place un système de navette qui les amène au travail.

– Si l’employé est à l’heure un jour donné, la probabilité qu’il soit en retard le lendemain est $\dfrac{1}{5}$ .

– S’il est en retard un jour donné, la probabilité qu’il soit en retard le lendemain est $\dfrac{1}{20}$ .

Pour tout entier naturel non $n$ , on appelle $R_n$ l’événement “l’employé est en retard le jour $n$ ” et $\overline{R_n}$ son événement contraire. On note $p_n$ la probabilité $R_n$ et $q_n$ celle de $\overline{R_n}$ .