Entraînement 2/8 – oral inspecteur DGFIP

Dryss 6 commentaires
Partager l'article
 
3   

Et voici enfin le deuxième entraînement pour l’oral d’inspecteur de la DGFIP ! L’attente, je l’admets, a été un peu longue. Je ne cache pas que j’ai eu beaucoup à faire de mon côté en vue de préparer un examen personnel. Mais maintenant que je suis en vacances pour deux semaines, ça devrait être un peu plus régulier (dit celui qui n’a pas compris que les fêtes vont beaucoup l’occuper !).

Correction de l’entraînement oral 1

Pour commencer, la correction de l’entraînement de la fois passée. Un exercice sur les complexes, un autre sur l’arithmétique. Vous pouvez retrouver le sujet ici.

Pour le premier, j’ai pris le parti de démontrer que chaque proposition était équivalente à la 2. C’est un choix tout à fait personnel, qui me semble le plus simple, mais si vous avez eu d’autres intuitions je suis preneur ! Notamment si certains ont cherché à faire une démonstration circulaire (du type 1 \Longrightarrow 2 \Longrightarrow 3 \Longrightarrow 4 \Longrightarrow 1)

Pour le second, j’ai proposé deux résolutions, l’une se basant sur une distinction de cas, l’autre sur une modification de l’écriture donnée dans l’énoncé. Pour ma part, à l’oral, j’avais choisi la première façon. Comme je l’avais annoncé dans l’article sur mes conseils pour l’oral, je n’avais pas rédigé entièrement la correction de celui-ci au tableau lors de mon passage, mais simplement les cas où n \equiv 0 [2] pair, et celui où n \equiv 1 [3], expliquant les autres oralement.

Correction Entraînement Oral 1

Petit avant-propos

Aujourd’hui, je vous propose un exercice de matrice et un d’analyse de fonction. Pour ne rien vous cacher, le premier est vraiment rude, le second plus direct.

Pour rappel, voici la façon dont je vous propose d’aborder cet entraînement :

Réservez vingt minutes de votre temps, comme dans les conditions d’examen. Mettez un chrono s’il le faut. Dès que vous aurez lu les exercices que je propose, déclenchez le chrono et faites les. 20  minutes, et pas une de plus. Une fois terminé, si vous pensez avoir réussi, allez directement à la correction pour comparer les résultats. Si par contre vous  avez eu des difficultés, voire n’avez pas réussi à faire une question, consultez la partie Coup de pouce. Ça représente les idées que pourraient vous donner le jury pour tenter de vous aiguiller dans la réponse.

Vous êtes prêt ? C’est parti 🙂 Bon courage !

Le sujet

EXERCICE 1

Soit 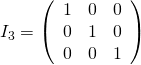I_3 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) et U_3 = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right).

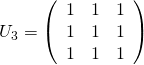De plus, on pose 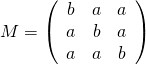M = \left( \begin{array}{ccc} b & a & a \\ a & b & a \\ a & a & b \end{array}\right) avec a et b deux réels.

Calculer M^n pour tout n \in \mathbb{N}^*.

EXERCICE 2

Soit P(x) = a_0 + a_1 x + a_2 x^2 + ... + a_nx^n défini pour tout x \in \mathbb{R}.

On suppose que a_0 + \dfrac{a_1}{2} + \dfrac{a_2}{3} + ... + \dfrac{a_n}{n+1} = 0

Démontrer qu’il existe x \in ]0 ; 1[ tel que P(x) = 0.

Coup de Pouce

EXERCICE 1

Calculer tout d’abord U^n pour n \in \mathbb{N}^*

Attention, dans un exercice de matrices, à bien énoncer pourquoi on peut utiliser le binôme de Newton

Exercice très calculatoire, bien faire attention à toutes les étapes

Deux astuces de calculs interviennent : m = m + n - n et m^{n-1} = \dfrac{m^n}{m}.

[collapse]

EXERCICE 2

Étant donné l’hypothèse faite dans l’exercice, on peut supposer que c’est grâce à une fonction “auxiliaire” de P qu’on peut répondre à la question. Laquelle ?

Quels sont les théorèmes au programme qui permettent de démontrer qu’il existe un x tels que f(x) = 0 ? Il y en a deux fondamentaux : Le théorème des valeurs intermédiaires et Le théorème de Rolle. On pourrait aussi dire qu’il y a le théorèmes des accroissements finis, généralisation du théorème de Rolle.

[collapse]

Conclusion

Encore une fois, je ne mettrai pas la correction de ce sujet aujourd’hui, mais sur le prochain billet (qui devrait venir un peu plus rapidement que celui-ci !). D’ici là, n’hésitez pas : en cas de doute, d’incertitude, voire d’incompréhension, posez vos questions en commentaires pour que je puisse y répondre ! Et mieux encore, si vous voulez vous tenir informés de la sortie des prochains billets, je vous propose de suivre la page Facebook de 19 en maths !

En attendant, j’imagine que le stress qui commence à monter. Mais oubliez ça pendant quelques jours durant cette période ! Je vous souhaite à tous d’excellentes fêtes ! Et tout en vous rappelant que l’abus de chocolat n’est pas une bonne idée :p


Partager l'article
 
3   
 
3
Partages
3   

6 commentaires

  1. Bonsoir. Tout d’abord un grand merci pour ce blog ! J’ai essayé de résoudre l’exercice 1. A l’aide du binôme de Newton, j’aboutis à un résultat mais je ne sais pas s’il est correct. Peut-être que l’expression que j’ai obtenue est bonne mais davantage simplifiable. Notamment je ne comprends pas où intervient le calcul m=m+n-n. Malheureusement, je ne peux pas écrire ce que j’ai trouvé ici. Pour remédier à ce petit contretemps, j’envoie un pdf par mail à l’administrateur de ce blog qui, j’en suis sûr, relaiera cette information. Bonne soirée et joyeuses fêtes à tous !

    • Répondu ! Pour information, il faut tenter de trouver une expression “simple” qui ne fait plus intervenir le symbole somme. Autrement dit, la formule dépendant de U et I, il faut trouver les coefficients qui vont avec ces deux matrices.

      La correction de l’exercice vient d’arriver, tu pourras la trouver ici : https://19enmaths.fr/oral-3-inspecteur-finances-publiques/

      Merci sinon pour le compliment 🙂 J’espère que ça vous aidera pour l’oral !

  2. Bonjour, tout d’abord merci pour les conseils et pour “l’entrainement”
    Pour l’exercice, j’ai procédé par implication ( 1 ; 4 ; 2 ; 3 ), mais je “coincé” sur le 3 implique 1 . Merci pour ta méthode, elle est plus rapide
    Pour l’exercice 2, avec un tableau de congruence , l’exercice se résout facilement en 2 minutes et 3 lignes….

    • Pour l’exercice 2, effectivement, il était vraiment très simple (dès lors qu’on connaît les quelques définitions primaires sur l’arithmétique). Pour le un, le 3 implique 1 nécessite une sacrée dose d’intuition à mon avis ^^ Content de voir que ma correction a pu servir !

  3. pour la série 2 :
    Merci pour la solution de l’exercice 1 , en effet je m’étais arrêté à l’étape (5) ….je n’avais pas pensé à la suite ( dans le temps imparti !)
    Pour l’exercice 2, j’ai procédé de la même façon , sauf la conclusion, j’ai utilisé le théorème sur la moyenne pour une intégrale….mais le théorème de Rolle était bien vu !!

    • Dans le cas où vous n’iriez pas assez loin dans la résolution, le jury vous le fera remarquer. À la condition absolue de ne pas effacer le tableau lors des 7 premières minutes, comme je l’indique dans Cinq conseils pour réussir l’oral de maths.

      Pour l’exercice 2, comme je le dis toujours, je propose une solution personnelle, mais elle n’est souvent pas l’unique moyen de faire ! Seule la solution l’est, donc toute approche qui mène à la même solution peut aussi être valable. Sauf si, bien sûr, il y a erreur dans mon propre corrigé !

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur comment les données de vos commentaires sont utilisées.