C’est parti maintenant pour un exercice de géométrie ! En regardant les sujets des derniers concours de contrôleur des finances publiques, on remarque que c’est aussi un exercice qui tombe souvent, mais uniquement dans la version géométrie dans l’espace.
Je ne sais pas pourquoi, la géométrie a souvent mauvaise presse parmi les candidats. Je soupçonne comme une espèce de rancœur tenace des terribles cours de quatrième sur les véritables premiers exercices de géométrie (oui, rappelez-vous, avec “données, propriété, conclusion” et la rédaction tant redoutée !). C’est vrai qu’à l’époque, c’était rude. Moi-même, en tant qu’enseignant, j’ai toujours tout tenté pour rendre la géométrie moins abrupte pour mes élèves de collège. Avec un succès… hum… disons relatif ! *Ahem*
Seulement, à partir d’un certain niveau (vers la classe de Seconde), la géométrie devient principalement analytique. Sous couvert d’un gros mot, ça veut simplement dire que ce qu’on nous demande de démontrer va principalement se faire grâce à des calculs et des résolutions d’équations, et non plus par des propriétés à connaître et à appliquer. Pour ne rien vous cacher, à mes yeux, la géométrie analytique perd son charme premier, mais je reviendrai dans un futur billet sur mon amour inconditionnel de cette partie des mathématiques (et de ma haine viscérale de l’analyse de fonction).
Je vous propose donc un petit exercice, toujours pris dans un sujet de Contrôleur des Finances Publiques, millésime 2014 cette fois. Cet exercice a le mérite d’être court, et de faire appel à deux notions essentielles qu’il faut absolument maîtriser pour les concours. À savoir, le produit scalaire de vecteur (programme de Première), et le produit vectoriel (qui a disparu des programmes de lycée, ce qui est bien dommage pour nos amis les physiciens surtout).
Évidemment, comme d’habitude, pas de correction avant d’avoir tenté de résoudre la question !
Énoncé de l’exercice
Dans l’espace rapporté à un repère orthonormal ![]() , on considère les points
, on considère les points
![]()
1/ a) Montrer que les points ![]() ,
, ![]() et
et ![]() ne sont pas alignés, et que le triangle
ne sont pas alignés, et que le triangle ![]() est isocèle et rectangle.
est isocèle et rectangle.
b) Montrer que le vecteur ![]() est un vecteur normal au plan
est un vecteur normal au plan ![]() .
.
c) En déduire une équation du plan ![]() .
.
2/ Soient ![]() et
et ![]() les plans d’équations respectives
les plans d’équations respectives ![]() et
et ![]() .
.
a) Montrer que les plans ![]() et
et ![]() sont sécants, et que leur intersection est une droite dont on précisera l’équation.
sont sécants, et que leur intersection est une droite dont on précisera l’équation.
b)Montrer que les plans ![]() ,
, ![]() et
et ![]() ont un unique point d’intersection dont on déterminera les coordonnées.
ont un unique point d’intersection dont on déterminera les coordonnées.
Coup de pouce
1/ a) Pour démontrer que trois points ne sont pas alignés, on démontre que deux vecteurs partageant un point commun ne sont pas colinéaires ;
De plus, pour démontrer qu’un triangle est rectangle, on utilise le produit scalaire (la seule véritable utilité du produit scalaire !)
Enfin, pour calculer la norme d’un vecteur dans l’espace, on a la formule qui ressemble beaucoup à celle de Pythagore, à savoir ![]() .
.
b) Deux possibilités : soit on utilise deux fois le produit scalaire avec deux vecteurs non orthogonaux du plan ![]() , soit (quand l’énoncé vicieux ne donne pas les coordonnées du vecteur à trouver), on utilise le produit vectoriel (qui est au programme du concours !)
, soit (quand l’énoncé vicieux ne donne pas les coordonnées du vecteur à trouver), on utilise le produit vectoriel (qui est au programme du concours !)
![Rendered by QuickLaTeX.com \[\vec{a} \wedge \vec{b} = \left( \begin{array}{c} y_{\vec{a}} \times z_{\vec{b}} - y_{\vec{b}} \times z_{\vec{a}} \\ z_{\vec{a}} \times x_{\vec{b}} - z_{\vec{b}} \times x_{\vec{a}} \\ x_{\vec{a}} \times y_{\vec{b}} - x_{\vec{b}} \times y_{\vec{a}} \end{array} \right)\]](https://19enmaths.fr/wp-content/ql-cache/quicklatex.com-ea47dfa7c4cb0bac369a7ccbf8342d07_l3.png)
c) Quand on a les coordonnées d’un vecteur normal au plan, de la forme 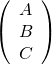 , l’équation du plan est de la forme
, l’équation du plan est de la forme ![]() . Puis il faut déterminer
. Puis il faut déterminer ![]() .
.
2/ a) Deux plans sont sécants en une droite si leurs vecteurs normaux ne sont pas parallèles. Puis on résout un système pour trouver une équation paramétrique de la droite.
b) Un plan et une droite sont sécants en un point si un vecteur normal du plan et un vecteur directeur de la droite ne sont pas orthogonaux. Puis on résout un système pour obtenir les coordonnées du point.