Ca y est, c’est le dernier jour ! À partir de demain, les oraux vont commencer pour vous. Je vous souhaite de nouveau tout le courage nécessaire pour affronter ces épreuves ! C’est donc ici que se termine cette série d’entraînement à l’oral de maths, qui je l’espère vous sera utile pour cette semaine !
Correction de l’entraînement oral 6
Dans le sujet proposé, j’avais choisi deux exercices pour une petite révision de méthodes. Tout d’abord, dans l’exercice 1, je souhaitais revoir les fractions rationnelles, avec les trois principales façons de les aborder : lorsqu’on a que des pôles simples dans ![]() , lorsqu’on a des pôles multiples dans
, lorsqu’on a des pôles multiples dans ![]() , et enfin lorsque la décomposition se fait dans
, et enfin lorsque la décomposition se fait dans ![]() . Cette dernière fait intervenir un théorème important des fonctions rationnelles, c’est à dire la “formule des résidus” (qui est connue sous différents noms, mais celui-ci est le plus courant).
. Cette dernière fait intervenir un théorème important des fonctions rationnelles, c’est à dire la “formule des résidus” (qui est connue sous différents noms, mais celui-ci est le plus courant).
Dans l’exercice 2 cette fois, qui était de nouveau un exercice d’arithmétique, je reprenais cette fois principalement le petit théorème de Fermat, et une démonstration de type “Par l’absurde” pour résoudre l’exercice.
Correction Entraînement 6 – Oral Inspecteur des Finances Publiques (version corrigée)
Avant propos
Pour conclure la série des entraînements, je vais cette fois-ci prendre deux sujets que je n’avais pas encore abordé. Le premier porte sur un exercice “de géométrie” (je mets des guillemets car la résolution de celui-ci passe finalement plus par du calcul que par de la géométrie véritable), le second sur un exercice à propos des intégrales, pour rappeler les principaux cas que vous pourrez rencontrer afin de résoudre simplement ces exercices. Ces deux énoncés ont été pris dans une liste d’exercices pour khôlle de MPSI.
Le sujet
EXERCICE 1
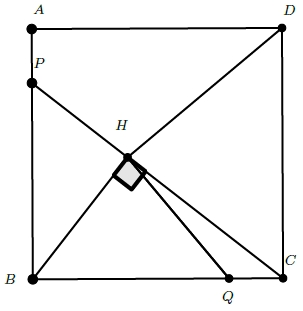
Soit ![]() un carré. On construit
un carré. On construit ![]() et
et ![]() tels que
tels que ![]() . Soit
. Soit ![]() le projeté orthogonal de
le projeté orthogonal de ![]() sur
sur ![]() .
.
Montrer que ![]() et
et ![]() sont orthogonales.
sont orthogonales.
EXERCICE 2
Calculer les intégrales suivantes :
1/ I = ![]()
2/ J = ![]()
3/ K![]() avec
avec ![]() un entier naturel supérieur ou égal à 2
un entier naturel supérieur ou égal à 2
4/ L = ![]()
Coup de pouce
On résout cet exercice en passant par de la géométrie analytique. Prendre le repère ![]() , et exprimer les coordonnées de tous les points dans ce repère.
, et exprimer les coordonnées de tous les points dans ce repère.
Puis se rappeler que démontrer que ![]() est orthogonale à
est orthogonale à ![]() revient à démontrer que
revient à démontrer que ![]() .
.
1/ Il s’agit d’un jeu d’écriture : ![]()
2/ On utilise une intégration par partie.
3/ On utilise un changement de variable “bien choisi” : ici, ![]() .
.
4/ On utilise les règles de Bioche pour trouver le bon changement de variable.
Conclusion
Et oui, pour cette dernière fois, je vais mettre la correction du sujet ! Vous y retrouverez surtout deux rappels concernant les règles du “LPET” et celles de Bioche pour le calcul des intégrales, qui peuvent de nouveau faire une différence face au jury si vous en avez au moins la connaissance.
Correction entraînement oral – Inspecteur des finances publiques (version corrigée)
Pour conclure, j’espère que tous ces entraînements vous auront permis de vous rafraîchir la mémoire (voire de vous faire revenir sur certaines notions non maîtrisées ^^), et je vous souhaite maintenant de vous retrouver l’année prochaine parmi les collègues de la maison ! Et bien sûr, n’hésitez surtout pas à me faire un retour sur votre ressenti de cette épreuve, ça me fera l’occasion de vous mettre à l’honneur sur un billet l’an prochain 🙂
Bonjour,
Merci encore pour tous ces exos.
Dans la correction de l’exo 2, question 2, il n’y aurait pas une erreur dans la deuxième partie de l’intégration par partie ?
Oh si, une énorme même 🙂 j’ai vérifié douze fois mes règles de Bioche pour être certain de ne pas me tromper et je fais une erreur de débutant dans l’IPP ^^ je reprends ça dès que je suis sur mon pc.
Bon courage pour cette semaine !
Salut,
Je crois qu’il manque les i dans les exposants de tes exponentielles complexes dans la correction 6/7 de l’exo 1 question 2 (les solutions omega k). Merci encore pour cet entrainement !
Bien vu ! Merci pour ta veille, c’est corrigé !
J’espère que l’oral s’est bien passé !
Pas encore, vendredi ^^
Bonjour
Je prépare le concours d inspecteur des finances publiques, je ne trouve assez d annales pour réviser les maths.
Comment puis je accéder à vos exercices des le début i.e la page 1/1???
Bonjour Christine,
Avant tout, merci pour l’intérêt que vous portez au site ! J’espère qu’il a pu vous aider dans vos révisions. Désolé aussi pour le délai de ma réponse, mais j’ai été un peu pris par des vacances intenses 🙂
Sinon, les exercices de mathématiques pour le concours d’inspecteur peuvent être retrouvés grâce à la bannière tout en haut du site : en cliquant sur inspecteur, un menu déroulant propose “Oral – Cat A”, puis les différents thèmes qui ont déjà été abordés : les exercices sont cachés dedans !
À l’heure actuelle, je n’ai pas encore proposé d’exercice pour l’écrit (quand bien même ceux de l’oral permettent tout de même de le réviser), mais vous trouverez sur le lien suivant quelques exercices corrigés des sessions précédentes : https://www.dropbox.com/sh/lulwkmtv2tbrb3e/AADrSqDY-u295oePKO321rPNa?dl=0
Bon courage pour le concours !